Korrelation ist ein Begriff, der die statistische Abhängigkeit zwischen mindestens zwei Parametern beschreibt.
Wozu dient Korrelation?
Korrelation dient dazu, die statistische Abhängigkeit einer abhängigen Variablen (die wir herausfinden möchten) von einer unabhängigen Variablen (die wir kennen oder einstellen können) zu bestimmen. Korrelation wird meistens verwendet, um den Wert der abhängigen Variablen zu schätzen, also um einen bestimmten Zustand vorherzusagen. Es handelt sich um ein einfaches statistisches Modell eines Systems.
Die Korrelation kann einfach sein, wobei der Zusammenhang zwischen einer unabhängigen und einer abhängigen Variablen bestimmt wird. Dies ist der häufigste Typ der Korrelation.
Komplexer sind die sogenannten multiplen Korrelationen, die den Zusammenhang einer abhängigen Variablen von mehreren unabhängigen Variablen beschreiben.
Für die Korrelation gelten Einschränkungen aufgrund ihrer Natur. Korrelation beschreibt ausschließlich eine statistische Abhängigkeit, keine kausale. Zwischen der unabhängigen und der abhängigen Variablen muss kein direkter Zusammenhang bestehen.
Der Unterschied zwischen kausaler und statistischer Abhängigkeit kann anhand des folgenden Beispiels demonstriert werden:
In New York wurden verschiedene Faktoren in Bezug auf Kriminalität untersucht, und es wurde festgestellt, dass eine starke Korrelation zwischen der Anzahl verkaufter Eiscreme und der Anzahl von Wohnungseinbrüchen besteht. Wenn die Anzahl verkaufter Eiscreme zunahm, nahm auch die Anzahl der Einbrüche zu. Trotz einer starken statistischen Korrelation besteht kein kausaler Zusammenhang zwischen dem Verkauf von Eiscreme und der Anzahl der Einbrüche.
Eine weitere Einschränkung ist, dass die Werte der abhängigen Variablen nur innerhalb des Bereichs der unabhängigen Variablen vorhergesagt werden können, in dem die statistische Abhängigkeit bestimmt wurde. Zum Beispiel, wenn ich die Lufttemperatur in Abhängigkeit von der Tageszeit im Monat Juni messe, kann ich die Temperaturen zu einer bestimmten Stunde nur für den Monat Juni schätzen. Für den Monat Januar kann ich die Schätzwerte nicht verwenden.
Da die Korrelation eine sogenannte statistische Abhängigkeit und keine kausale (Ursache-Wirkung) beschreibt, kann auch bei einer starken Korrelation der Wert einer unbekannten Variablen nicht mit 100%iger Sicherheit bestimmt werden.
Verwendung in der Praxis
Die Untersuchung der Korrelation kann durchgeführt werden, nachdem eine ausreichende Anzahl von Messwerten der abhängigen und unabhängigen Variablen gleichzeitig erfasst wurde. Im zweiten Schritt wird die Korrelation zwischen der abhängigen Variable und der/den unabhängigen Variablen bestimmt. Die Enge der Korrelation (Korrelationseffekt) und die Form der Kurve, die die Abhängigkeit darstellt, werden untersucht. Im einfachsten Fall beschreibt die Beziehung zwischen der abhängigen und einer unabhängigen Variablen eine Gerade. In diesem Fall sprechen wir von einer linearen Abhängigkeit. Die Beziehung wird durch die Gleichung der Geraden in der Form y = ax+b ausgedrückt, wobei y die abhängige Variable und x die unabhängige Variable ist.
Zur Bestimmung der Enge der Korrelation wird der Korrelationskoeffizient verwendet, der Werte von -1 bis 1 annimmt. In der Praxis wird das Quadrat des Korrelationskoeffizienten verwendet. Wenn der Korrelationskoeffizient positiv ist, besteht zwischen den Variablen eine direkte Proportionalität. Wenn er negativ ist, besteht eine indirekte Proportionalität. Wenn der Koeffizient gleich null ist, sind beide Variablen statistisch unabhängig.
Eine grafische Darstellung der Abhängigkeit ist das Korrelationsdiagramm, bei dem auf der x-Achse die Werte der unabhängigen Variablen und auf der y-Achse die der abhängigen Variablen aufgetragen werden. Die gemessenen Punkte werden durch eine sogenannte Regressionskurve verbunden, die die Funktion der Abhängigkeit der Variablen darstellt. Ihre "Genauigkeit" wird durch den Korrelationskoeffizienten bzw. dessen Quadrat ausgedrückt. Je näher der Wert des Quadrats bei 1 liegt, desto genauer kann der Wert der abhängigen Variablen aus dem Wert der unabhängigen Variablen gemäß der Regressionsgleichung bestimmt werden. Wenn der Korrelationskoeffizient gleich null ist (sein Quadrat ist dann ebenfalls null), kann der Wert der abhängigen Variablen nicht aus dem Wert der unabhängigen Variablen bestimmt werden. Die abhängige Variable verhält sich wie eine Zufallsvariable, deren Wert nicht durch den Wert der unabhängigen Variablen beeinflusst wird.
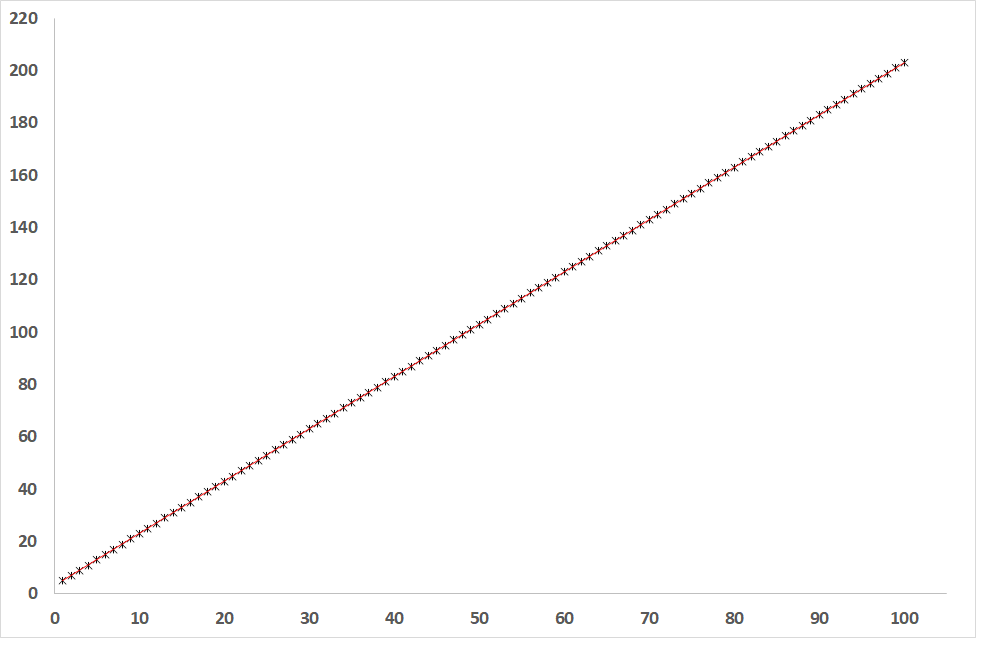
Abb. 1: Abhängigkeit der abhängigen Variablen von der unabhängigen Variablen, wenn R = 1 (Gerade der direkten Proportionalität)
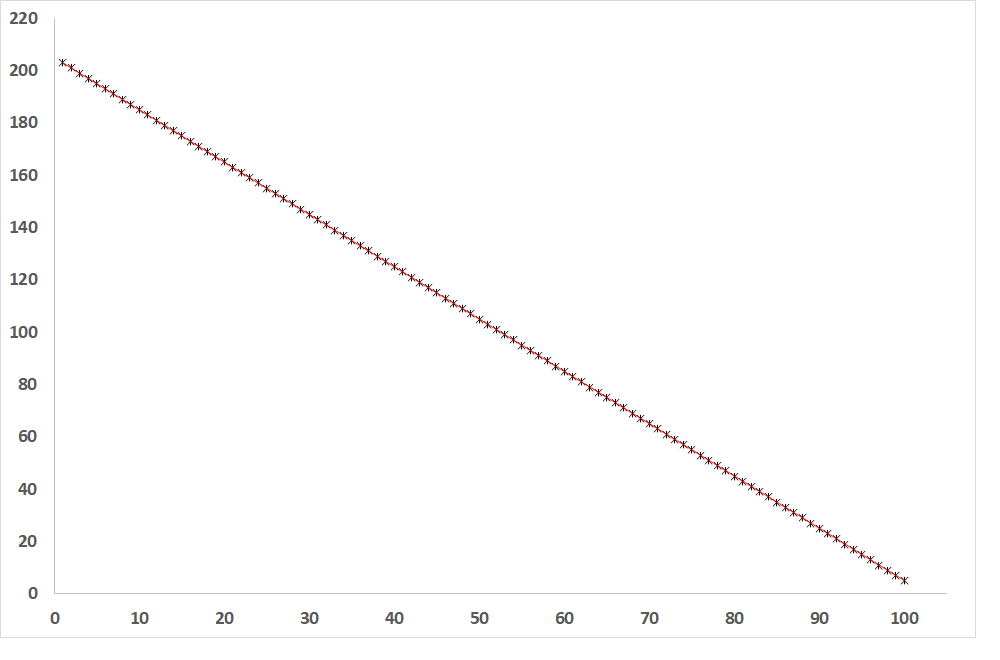
Abb. 2: Abhängigkeit der abhängigen Variablen von der unabhängigen Variablen, wenn R = -1 (Gerade der indirekten Proportionalität)
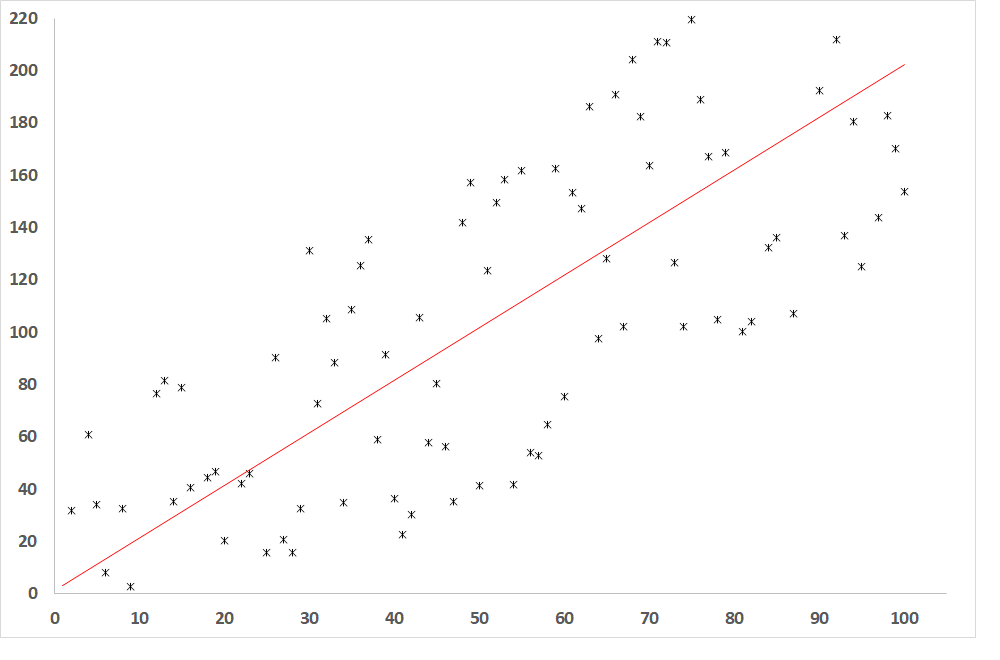
Abb. 3: Abhängigkeit der abhängigen Variablen von der unabhängigen Variablen, wenn R = 0,8 (relativ enger Zusammenhang zwischen den Variablen)
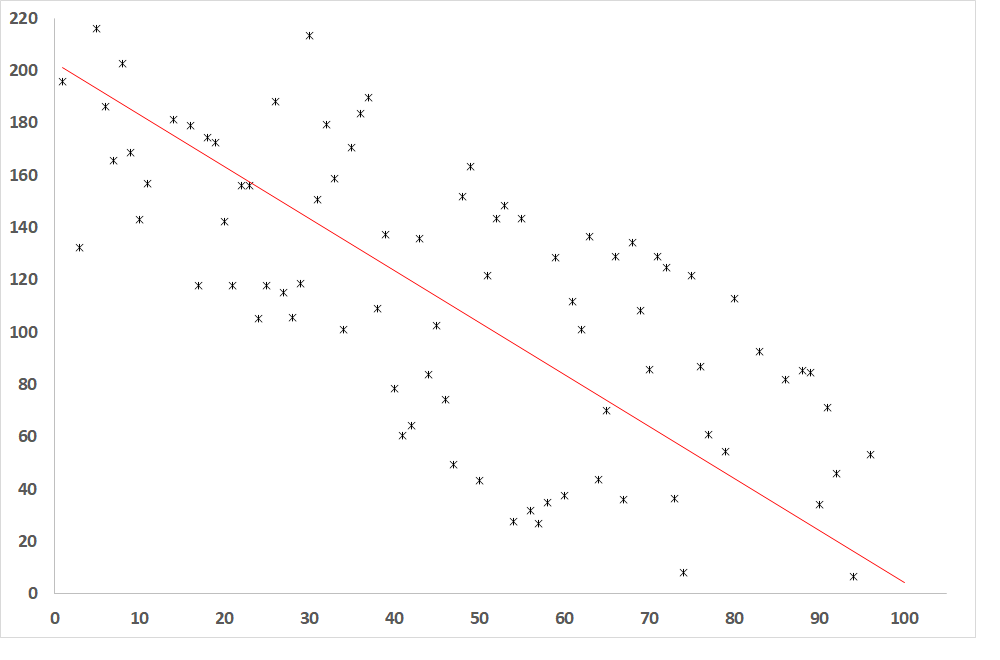
Abb. 4: Abhängigkeit der abhängigen Variablen von der unabhängigen Variablen, wenn R = -0,8 (relativ enger Zusammenhang zwischen den Variablen)
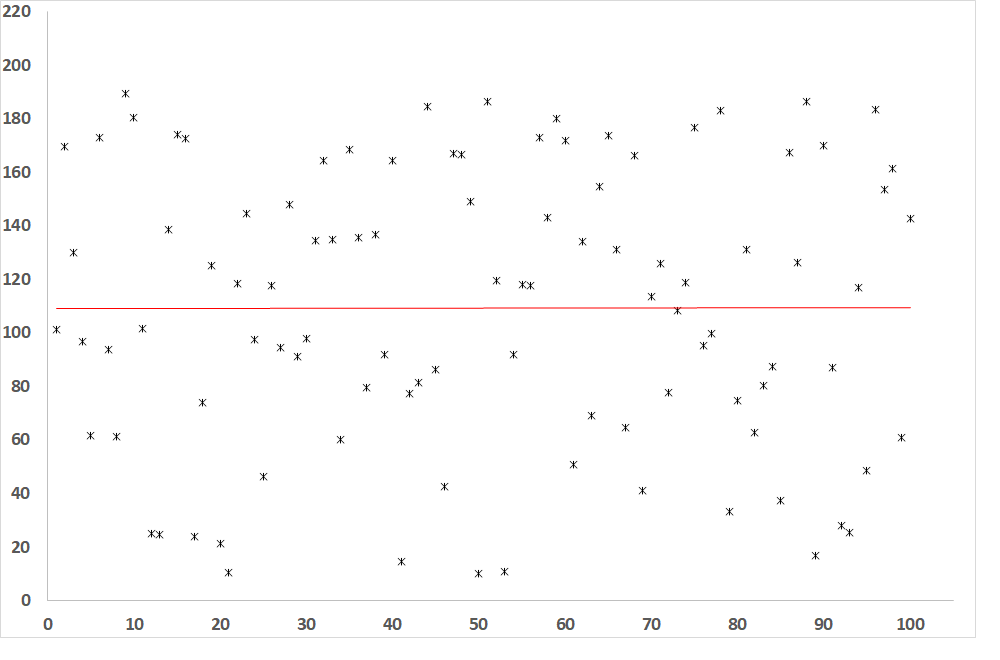
Abb. 5: Abhängigkeit der abhängigen Variablen von der unabhängigen Variablen, wenn R = 0 (keine Korrelation zwischen den Variablen)
Das Thema Korrelation ist umfangreich, dieser Artikel ist eine kurze Zusammenfassung. Für ein tieferes Studium empfehlen wir die Teilnahme an einer unserer Schulungen.
Empfohlene Schulungen:
| Titel der Schulung | Dauer der Schulung | Verfügbare Termine | Preis | |
|---|---|---|---|---|
| Innovative Methoden in der Automobilindustrie und im Maschinenbau |
11 Tage
|
04.05.2026
+ 2 verfügbare Termine
|
4 890,00 €
5 819,10 € inkl. MwSt
|
Mehr über die Schulung |
| Grundlagen von SPC - Statistische Methoden zur Prozesssteuerung |
2 Tag
|
12.05.2026
+ 5 verfügbare Termine
|
980,00 €
1 166,20 € inkl. MwSt
|
Mehr über die Schulung |
| SPC II - SPC Problembehedung |
2 Tage
|
Ihrer Meinung nach
|
Auf Anforderung | Mehr über die Schulung |
| Six Sigma-Schulung |
2 Tage
|
Ihrer Meinung nach
|
Auf Anforderung | Mehr über die Schulung |
| SPC III – Einführung statistischer Methoden in der Organisation |
2 Tage
|
Ihrer Meinung nach
|
Auf Anforderung | Mehr über die Schulung |